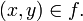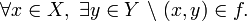La habitacion de Fermat

Sipnosis:

Un joven de 22 años cuyo nombre no se desvela en la película (su pseudónimo es Galois), está esperando que llegue el 20 de febrero para presentar su demostración de la conjetura de Goldbach. Mientras explica en qué consiste la conjetura de Golbach a unas amigas, unos chicos lo llaman para que Galois suba a su habitación. Al llegar lo encuentra todo destrozado: algún misterioso personaje ha saboteado la demostración.

ar

Mientras tanto, otro personaje (conocido por Hilbert) mientras juega al ajedrez comenta a su amigo médico que hace tiempo intentó suicidarse. También le dice que ha recibido una carta en la que le invitan a pasar un fin de semana con las mentes matemáticas más ingeniosas del país, con el pretexto de resolver un gran enigma. Para ello es necesario que descubra en qué orden están los números: 5-4-2-9-8-6-7-3-1.

Pascal, pseudónimo por el que se conoce al tercer personaje, recibe la misma carta. Se encuentra pensando el acertijo en una biblioteca. Tras muchas horas intentando resolverlo se da por vencido y rompe la hoja. Pero la bibliotecaria le dice que los libros que use los deje en su orden alfabético. La palabra "alfabético" resulta ser una pista fundamental y tras leer la palabra "orden" inmediatamente obtiene tiene la respuesta: Cinco. Cuatro. Dos. Nueve. Ocho. Seis. Siete. Tres. Uno. Los números estaban colocados por orden alfabético. Pascal envía el resultado al apartado de correos 325 y recibe una segunda carta en la que le cita para que acuda a un lugar.

Cuando Pascal llega a ese lugar no hay nadie. Después de él llega Oliva, una joven de 26 años, que había recibido la misma carta. A continuación, llegan Hilbert y Galois en el mismo coche. El lugar está junto a un enorme lago.

A las 19:00 PM, las luces de un coche parpadean en la otra orilla. Encuentran una barca y cruzan el lago. Se montan en el coche y mediante una agenda PDA encuentran el lugar donde se va a producir la reunión: una granja avícola. Entran en ella y llegan a una habitación bellamente decorada, dispone de todo lo que Hilbert fue echando en falta en medio de aquel ruinoso edificio.

Después de un rato esperando, llega el esperado anfitrión: Fermat. Cenan y después de ello Fermat recibe una llamada telefónica del hospital. Únicamente le dicen: «Buenas noches señor Naranjo, le llamo del hospital. Un momento por favor». Dado que él tiene a su hija en coma abandona apresuradamente la reunión para dirigirse hasta el hospital.

Es entonces cuando se les formulan a los asistentes una serie de acertijos mediante la PDA. Si no los aciertan en menos de un minuto la habitación empieza a encoger.

Mientras resuelven algunos de los acertijos, descubren que Fermat no era el anfitrión sino una cabeza de turco. Todo había sido meticulosamente planeado por Hilbert, que había fingido ser un invitado más. Lo había hecho, según él, para vengarse de Galois (que había resuelto la conjetura de Goldbach y había arruinado el trabajo de su vida). Galois confiesa que él realmente no la había resuelto. Tan solo se había inventado esa gran mentira para volver con Oliva, ya que hace tiempo había roto con ella.

Cuando la habitación está a punto de aplastarlos a todos, los tres protagonistas consiguen escizapar por un pasado situado detrás de una pizarra que el propio Hilbert había creado para salir en caso de emergencia. Hilbert se queda dentro inconsciente, Galois le había propinado un puñetazo en un ataque de ira.

Al salir, mientras vuelven en la barca, Pascal tira al lago los papeles en los que Hilbert resolvía la conjetura de Goldbach. Galois le pregunta por qué le ha hecho eso al mundo, a lo que Pascal responde que «el mundo está como estaba»

Problemas y soluciones:

1.-¿Qué tienen en común Georg Cantor, Yutaka Taniyama y Kurt Gödel?

       Solucion: Los tres enloquecieron y se suicidaron

2.-¿Qué patrón sigue la siguiente secuencia de números   5 – 4 – 2 – 9 – 8 – 6 – 7 – 3 – 1?

       Solución:Estan colocados segun el alfabeto 

3.-Tres cajas opacas de caramelos aparecen etiquetadas en tres tipos: anís, menta y mezcla de ambas clases. Ninguno de estos rótulos está colocado en la caja correspondiente. ¿Cuántos caramelos debemos extraer de las cajas para colocar correctamente las etiquetas?

          Solución: un solo caramelo de la caja donde pone mezcla.

4.-Aparecen un montón de unos y ceros en la PDA. ¿Qué representan?

        Solucion: Una calavera

5.-el interior de una habitación hay una bombilla. Fuera hay tres interruptores, y sólo uno de ellos enciende la bombilla. Nosotros estamos fuera y sólo podemos entrar una vez a la habitación. ¿Cómo averiguar el interruptor que enciende la bombilla?
      Solucion:se enciende el primer interruptor, se deja un rato encendido.Despues se apaga y se enciende el segundo.Se entra en la habitacion...si la bombilla esta encendida es el segundo interruptos, si esta apaga pero caliente es el primero y si esta apagada pero fria es el tercero.
6.-¿Cómo medir exactamente 9 minutos con dos relojes de arena de 4 y 7 minutos?

        Solucion:Ponemos los dos relojes a la vez, el de 4 y el de 7. Cuando se termina la arena del de 4, han pasado 4 minutos. Le volvemos a dar la vuelta. Tres minutos después se acaba la arena del de 7. Le volvemos a dar la vuelta. Cuando se acaba la arena del de 4 por segunda vez han pasado 8 minutos. El de 7 ha cronometrado un minuto; le volvemos a dar la vuelta y ya tenemos los 9 minutos que nos piden.

7.-El conocido problema de la lechera y sus hijas, planteado aquí con otros personajes (un profesor y su alumno). Dos lecheras vecinas se encuentran en la calle. Una le pregunta a la otra por las edades de sus tres hijas, y la primera le indica: “El producto de las edades de mis tres hijas es 36 y su suma es el número del portal”. La vecina echa cálculos y al cabo de un rato le indica que le falta un dato. Tras repasar las cuentas, le dice, “En efecto. Mi hija mayor toca el piano” ¿Cuáles son las edades de las hijas?
       Solucion:9,2 y 2
8.-Un prisionero está en una celda guardada por dos carceleros que custodian sendas puertas. Una de estas puertas conduce a la libertad. Uno de los carceleros siempre dice la verdad y el otro siempre miente. Al prisionero se le permite hacer una única pregunta a uno de los dos guardianes. ¿Qué debe preguntar para salir de su encierro?

          Solucion:¿Qué puerta me diría tu compañero que es la buena?”

9.-Una madre es 21 años mayor que su hijo. Al cabo de 6 años la edad de la madre será cinco veces la que tenga el hijo. ¿Qué está haciendo el padre?

              Solucion:Según las condiciones del enunciado el hijo resulta tener  -3/4 (aparentemente una edad absurda, pero es necesario interpretarla), es decir, -9 meses, por lo que ya se sabe que hace el padre en esos momentos.

Critica 

   Creo que es una pelicula muy buena,que te hace pensar en las matematicas en algo util no solo en los cuadernos y muy entretenida.

  

Trigonometria

Introduccion:

La trigonometría es una rama de la matemática, cuyo significado etimológico es "la medición de los triángulos". Se deriva del vocablo griego τριγωνο "triángulo" + μετρον "medida".1
En términos generales, la trigonometría es el estudio de las funciones seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas de navegación por satélites.

Circunferencia goniometrica:

La circunferencia goniométrica, trigonométrica, unitaria o «círculo unidad» es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación.

Relaciones entre cuadrantes:

Identidades trigonométricas

cos² α + sen² α = 1

sec² α = 1 + tg² α

cosec² α = 1 + cotg² α









Suma y diferencia de ángulos







Ángulo doble





Ángulo mitad








Transformaciones de sumas en productos






Transformaciones de productos en sumas

Teorema de Napoleon

La habitación de Fermat

Teorema de Thales

Teorema de pitagoras

Concepto de función y propiedades.

Definición

   En matemáticas, una función, aplicación o mapeo f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el condominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por:

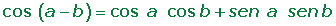
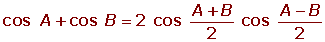
   Una función puede considerarse como un caso particular de una relación o de correspondencia matemática. Cada relación o correspondencia de un elemento con un (y sólo un) se denota , en lugar de
Formalmente, pedimos que se cumplan las siguientes dos condiciones:

1. Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir,
2. Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y, es decir, si

Propiedades de las funciones:

• Dominio :
• 
• Recorrido :
  
• Funciones simétricas :

-Simetría respecto del origen de coordenadas O(0,0)
Una función f es simétrica respecto del origen cuando para todo x del dominio se tiene

y se denominan funciones impares.
-Simetría respecto del eje de ordenadas OY
Una función f es simétrica respecto del eje de ordenadas cuando para todo x del dominio se tiene

y se denominan funciones pares.
-Simetría respecto del eje de abscisas OX
Dos funciones f y g son simétricas respecto del eje de abscisas si son funciones opuestas, es decir

-Simetría respecto de la bisectriz del 1º y 3º cuadrante

Dos funciones f y g son simétricas respecto de la bisectriz del 1º y 3º cuadrante si son funciones recíprocas, es decir

                           

La gráfica de una función par (impar) queda determinada si conocemos su forma para valores positivos de x , ya que la parte de la gráfica correspondiente a valores negativos de x se construye por simetría respecto del eje de ordenadas.

• Funciones periodicas :

Una función f es periódica de periodo T si

para todo x perteneciente al dominio de definición.
Las funciones periódicas más importantes son las funciones circulares seno, coseno y tangente.

• Continuidad :

Una función es continua en un punto si existe límite en dicho punto y coincide con el valor que toma la función en ese punto.

                         

• Regla de L´Hôpital (para funciones derivables)

•  Propiedades de los limites de las funciones:

Sean f y g dos funciones tales que existan
                    
y sea k un número real
                    
Estas relaciones son ciertas siempre que tengan sentido las operaciones definidas en la recta real. En caso contrario no es posible obtener el límite, cuando esto suceda diremos que es un caso de indeterminación.

• Indeterminaciones:

• Tabla de limites equivalentes:

• Asintotas :

-Horizontales

-Verticales

-Oblicuas