Definición
En matemáticas, una función, aplicación o mapeo f es una relación entre un conjunto dado X (el dominio) y otro conjunto de elementos Y (el condominio) de forma que a cada elemento x del dominio le corresponde un único elemento del codominio f(x). Se denota por:Una función puede considerarse como un caso particular de una relación o de correspondencia matemática. Cada relación o correspondencia de un elemento
 con un (y sólo un)
con un (y sólo un)  se denota
se denota  , en lugar de
, en lugar de 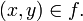
Formalmente, pedimos que se cumplan las siguientes dos condiciones:
- Condición de existencia: Todos los elementos de X están relacionados con elementos de Y, es decir,
- Condición de unicidad: Cada elemento de X está relacionado con un único elemento de Y, es decir, si
Propiedades de las funciones:
- Dominio :

- Recorrido :

- Funciones simétricas :
-Simetría respecto del origen de coordenadas O(0,0)
Una función f es simétrica respecto del origen cuando para todo x del dominio se tiene
y se denominan funciones impares.
-Simetría respecto del eje de ordenadas OY
Una función f es simétrica respecto del eje de ordenadas cuando para todo x del dominio se tiene
y se denominan funciones pares.
-Simetría respecto del eje de abscisas OX
Dos funciones f y g son simétricas respecto del eje de abscisas si son funciones opuestas, es decir
-Simetría respecto de la bisectriz del 1º y 3º cuadranteDos funciones f y g son simétricas respecto de la bisectriz del 1º y 3º cuadrante si son funciones recíprocas, es decir
La gráfica de una función par (impar) queda determinada si conocemos su forma para valores positivos de x , ya que la parte de la gráfica correspondiente a valores negativos de x se construye por simetría respecto del eje de ordenadas.
- Funciones periodicas :
Una función f es periódica de periodo T si
para todo x perteneciente al dominio de definición.
Las funciones periódicas más importantes son las funciones circulares seno, coseno y tangente.
- Continuidad :
Una función es continua en un punto si existe límite en dicho punto y coincide con el valor que toma la función en ese punto.
- Regla de L´Hôpital (para funciones derivables)
- Propiedades de los limites de las funciones:
Sean f y g dos funciones tales que existan
y sea k un número real
Estas relaciones son ciertas siempre que tengan sentido las operaciones definidas en la recta real. En caso contrario no es posible obtener el límite, cuando esto suceda diremos que es un caso de indeterminación.
- Indeterminaciones:
- Tabla de limites equivalentes:
- Asintotas :
-Horizontales
-Verticales
-Oblicuas

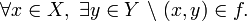





0 comentarios:
Publicar un comentario